Transformação de Galileu

As transformações de Galileu são utilizadas na comparação de fenómenos que ocorrem em referenciais inerciais distintos, dentro da física newtoniana ou mecânica clássica. Assim, conhecendo-se o estado de movimento num dado sistema de coordenadas, ao aplicarem-se as equações das transformações de Galileu, é possível expressar-se o estado desse movimento usando como referência outro sistema inercial.

Mais precisamente as transformações de Galileu permitem transformar as equações da física de um referencial inercial para outro, de forma a manter as equações invariantes (invariância galileana). Isto é, a forma das equações da física não pode depender do estado de movimento de um observador, uma vez que o movimento é relativo. Isto leva no entanto a contradições quando se considera as equações de Maxwell. A solução destas contradições levaram Albert Einstein a propor a Transformação de Lorentz com a transformação fundamental entre referênciais inerciais em movimento relativo.

Assim, se quiser achar as coordenadas de  a partir das coordenadas de  têm-se as equações: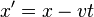

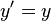
Relativo ao tempo, tem-se: