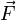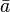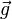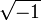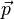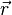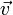Mecânica dos fluidos
A mecânica dos fluidos é a parte da física que estuda o efeito de forças em fluidos. Os fluidos em equilíbrio estático são estudados pela hidrostática e os fluidos sujeitos a forças externas diferentes de zero são estudados pela hidrodinâmica.1
Índice
[esconder]Propriedades físicas dos fluidos hidráulicos
As propriedades dos fluidos hidráulicos relevantes para o estudo do escoamento dos fluidos são a massa volúmica, a tensão superficial, a viscosidade, e restantespropriedades reológicas.
| Mecânica do contínuo Estudo da física de materiais contínuos | Mecânica dos sólidos Estudo da física de materiais contínuos com uma forma de repouso definida. | Elasticidade Descreve materiais que retornam à sua forma de repouso depois que as tensões aplicadas são removidas. | |
| Plasticidade Descreve materiais que se deformam permanentemente após uma tensão aplicada superar um determinado limite. | Reologia Estudo de materiais com características de sólido e fluido. | ||
| Mecânica dos fluidos Estudo da física de materiais contínuos que se deformam quando submetidos a uma força. | Fluidos não newtonianos não apresentam taxas de deformação proporcionais às tensões cisalhantes aplicadas. | ||
| Fluidos newtonianos apresentam taxas de deformação proporcionais às tensões cisalhantes aplicadas. | |||
Teoria
Os fluidos respeitam a conservação de massa, quantidade de movimento ou momentum linear e momentum angular, de energia, e deentropia. A conservação de quantidade de movimento é expressa pelas equações de Navier Stokes. Estas equações são deduzidas a partir de um balanço de forças/quantidade de movimento a um volume infinitesimal de fluido, também denominado de elemento representativo de volume.
Atualmente, o estudo, análise e compreensão da fenomenologia da maior parte dos problemas em dinâmica de fluidos e em transferência de calor, como macro-áreas que compõem a dinâmica de fluidos, são desenvolvidos através da Modelagem Computacional. Nesta, um modelo matemático é desenvolvido, com base na fenomenologia do problema considerado. A partir deste modelo, geralmente um sistema de equações diferenciais parciais ou equações diferenciais ordinárias, é desenvolvido um modelo computacional ou utilizado um código computacional comercial, para a execução de simulações numéricas, em fluidodinâmica computacional, obtendo-se assim projeções temporais da solução do problema. Esta solução é condicionado pelas condições iniciaise condições de contorno do problema, que estabelecem as condições de evolução deste no tempo e no espaço.
A Teoria do Contínuo fundamenta a conceituação teórica que justifica a maior parte das análise em CFD. O fluido, um meio contínuo, é discretizado com base no modelo das partículas fluidas. Esta abstração conceitua um elemento representativo de volume(representative element of volume, REV). Neste elemento de volume, de micro ou nano dimensões, uma propriedade ou quantidade física mantem um valor médio, sob as mesmas condições, passível de reprodução em laboratório, sob as mesmas solicitações externas ao fluido. Assim uma partícula representativa de um volume de fluido, o REV, é o menor volume em que as propriedades do fluido se mantém. As moléculas de um contínuo vibram constantemente, cessando esta vibração somente no estado de repouso termodinâmico, o zero absoluto. Fisicamente em um REV o caminho médio percorrido pelas moléculas do fluido entre duas sucessivas é no mínimo da ordem de grandeza das próprias moléculas deste fluido.
Hoje em dia os modernos aviões usam um artifício para driblar a formação de vórtices nas pontas das asas, como o winglet, um pequeno leme na extremidade da asa, permitindo que pelo menos um metro e meio de asa seja aproveitada na sustentação da aeronave, que é perdida para os vórtices que se formam na sua ausência. O vórtice ocorre quando o ar mais denso que flui abaixo da asa escapa para a parte superior menos densa, prejudicando sua sustentação naquela ponta de asa. Vórtices no sentido horário surgem na ponta da asa esquerda, anti-horário na asa direita. Nos profundores não se formam vórtices, pois não há diferença entre densidades do ar nos dois lados da empena.[carece de fontes]
Experiências recentes dão conta de que uma superfície irregular da fuselagem, tipo "bola de golfe", com aqueles sulcos em concha, tem mais fluidodinâmica do que a mesma superfície quando plana e polida. Este efeito se verifica com as asas das aves, onde a superfície apresenta um arrasto mínimo, mesmo com a aparente irregularidade das penas.
Também se faz experiência com bordos de ataque enrugados, tais como as nadadeiras de uma baleia, com reais vantagens para as mesmas áreas quando lisas e retas, por exemplo. Em ambos os casos, diminui-se a resistência do meio e melhora a performance e o consumo de energia de empuxo.
Os navios mais rápidos hoje construídos são aqueles em que o roda de proa (chapa enformada onde convergem a quilha, as balizas reviradas e as longarinas de proa; que é a parte do navio que corta a água) possui uma longa protuberância ogival abaixo da linha d'água, que permite uma excelente hidrodinâmica ao anular a formação das ondas com outras ondas de valores contrários.
Tipos de escoamentos
Os escoamentos podem ser classificados quanto à compressibilidade e quanto ao grau de mistura macroscópica.
Um escoamento em que a densidade do fluido varia significativamente é um escoamento compressível. Se a densidade não variar significativamente então o escoamento é incompressível.
O grau de mistura de um fluido em escoamento depende do regime de escoamento, que pode ser laminar, turbulento ou de transição.
No regime laminar, as linhas de fluxo são paralelas ao escoamento, fazendo com que o fluido escoe sem que ocorra mistura. Em um duto circular, o escoamento é laminar até um valor de Reynolds de aproximadamente 2100.
Na transição entre os regimes laminar e turbulento, percebe-se que as linhas de fluxo se tornam onduladas, o que indica que começa a haver mistura entre uma camada e outra. Para um duto circular, esse regime ocorre para um valor de Re entre 2100 e 2300.
Para valores de Re acima de 2300, têm-se regime turbulento. Nesta fase, percebe-se uma mistura entre as camadas de fluxo.
Métodos experimentais
O escoamento de fluidos é actualmente estudado por velocimetria laser e por velocimetria por imagem de partículas.
Abordagem computacional
A dinâmica de fluidos tem sido solicitada a fornecer soluções a problemas complexos em hidrodinâmica, projetos de edificações,aeronaves, navios e veículos espaciais, em hemodinâmica e em biofísica. Nestas áreas a obtenção e o de tratamento de soluções considera um elevado número de dados, informações e variáveis, resultando em densos sistemas de equações. A modelagem computacional propõe um conjunto de métodos e técnicas para a abordagem destes problemas.
Leis da Hidrodinâmica
Por forma a melhor compreender a física do deslocamento de fluidos em regime não turbulento, criou-se uma série de leis, que levaram à equação de Bernoulli. O que se estabelece segundo a equação é que
em que 
é um valor relativo e constante, 
é uma pressão relativa de outro ponto, 
corresponde à diferença de alturas entre eles, e 
à diferença de velocidades a que se encontram. A equação de Bernoulli está de certo modo relacionada com o porquê dos aviões voarem, e das garrafas de perfume expelirem líquido quando pressionadas.
é um valor relativo e constante, é uma pressão relativa de outro ponto, corresponde à diferença de alturas entre eles, e à diferença de velocidades a que se encontram. A equação de Bernoulli está de certo modo relacionada com o porquê dos aviões voarem, e das garrafas de perfume expelirem líquido quando pressionadas.
O que se passa com as asas do avião é que a sua periferia é feita de tal forma que o ar que passa por cima da asa tem que percorrer um maior percurso em relação ao ar que passa por baixo da asa. Ou seja, o ar sobre a asa move-se a uma velocidade maior. Dado este fato, a equação de Bernoulli prediz que a pressão acima da asa torna-se menor que abaixo da asa e, por este motivo, a uma determinada velocidade, a diferença de pressão é suficiente grande para fazer o avião levantar vôo.
A mecânica dos fluidos é a parte da física que estuda o efeito de forças em fluidos. Os fluidos em equilíbrio estático são estudados pela hidrostática e os fluidos sujeitos a forças externas diferentes de zero são estudados pela hidrodinâmica.1
Índice
[esconder]Propriedades físicas dos fluidos hidráulicos
As propriedades dos fluidos hidráulicos relevantes para o estudo do escoamento dos fluidos são a massa volúmica, a tensão superficial, a viscosidade, e restantespropriedades reológicas.
| Mecânica do contínuo Estudo da física de materiais contínuos | Mecânica dos sólidos Estudo da física de materiais contínuos com uma forma de repouso definida. | Elasticidade Descreve materiais que retornam à sua forma de repouso depois que as tensões aplicadas são removidas. | |
| Plasticidade Descreve materiais que se deformam permanentemente após uma tensão aplicada superar um determinado limite. | Reologia Estudo de materiais com características de sólido e fluido. | ||
| Mecânica dos fluidos Estudo da física de materiais contínuos que se deformam quando submetidos a uma força. | Fluidos não newtonianos não apresentam taxas de deformação proporcionais às tensões cisalhantes aplicadas. | ||
| Fluidos newtonianos apresentam taxas de deformação proporcionais às tensões cisalhantes aplicadas. | |||
O mesmo se passa no perfume: ao passar sobre a "boca" do frasco, o tubo estreita-se, sendo o ar nesse ponto obrigado a circular a uma velocidade maior. Assim, isso cria uma variação de pressão que empurra o perfume para a sua superfície, sendo depois disparado para o ar.
As equações de Bernoulli não possuem aplicação soberana na mecânica dos fluidos. As complexas Equações de Navier-Stokes são também utilizadas na análise da Mecânica dos fluidos.
Elas são não-lineares e com uma infinidade de soluções não-analíticas, ou seja, somente obtidas com aporte computacional. São equações que relacionam densidade dos fluidos, acelerações, variação de pressão, viscosidade e gradientes de velocidade.
Contudo, estas equações podem aproximar boas soluções algébricas quando feitas as devidas aproximações. Assumir, por exemplo, que o fluido é incompressível e sem viscosidade (idealização) faz com que estas equações sejam simplificadas e permitem soluções mais simples.
Ver artigo principal: 
durante um intervalo de tempo
