Mecânica clássica

A mecânica clássica se refere às três principais formulações da mecânica pré-relativística: amecânica newtoniana, mecânica lagrangeana e a mecânica hamiltoniana1 . É a parte da Físicaque analisa o movimento, as variações de energia e as forças que atuam sobre um corpo. No ensino de física, a mecânica clássica geralmente é a primeira área da física a ser lecionada. É geralmente classificada em estática, cinemática e dinâmica.

Índice

[esconder]

Teoria[editar | editar código-fonte]

A quantidade de problemas resolvidos a partir da mecânica clássica é grande, e isto acontece porque seus axiomas, ou princípios2 , são gerais. Dentre estes, os principais são:

O espaço é absoluto, imutável, não sofrendo alteração em função da matéria;
Da mesma forma que o espaço, o tempo também é absoluto, não sofrendo mudanças em função da matéria;
A velocidade de um corpo pode crescer ilimitadamente.

Unidades de medida[editar | editar código-fonte]

Ver artigo principal: Unidade de medida

O movimento de projéteis é estudado na mecânica clássica

Qualquer medida física só tem algum significado se for acompanhada da respectiva unidade e da incerteza do processo de medida.

A importância da unidade de medida é intuitiva: um texto que se refira a uma 'velocidade de 30' está claramente incompleto se não for especificada a unidade da velocidade, como em 'velocidade de 30 km/h' ou 'velocidade de 30 m/s'.

Já a incerteza do processo de medida é uma informação frequentemente negligenciada. Qualquer processo de medida possui uma incerteza inerente. Por exemplo, uma régua escolar é precisa até a unidade dos milímetros, e portanto qualquer medição feita com este instrumento deve ser registrada com esta informação. Ou seja, a medição efetuada com uma régua escolar tem um erro de aproximadamente 0,5 milímetros (é metade da divisão menor). Por exemplo, o comprimento de um determinado fio é 20 cm, dizemos que o seu comprimento é 20 ± 0,05 cm; logo, o comprimento exato do fio encontra-se entre 19,95 e 20,05 cm.

O erro de medida fica cada vez menor a medida que suas unidades são divididas em mais partes. Se, com a ajuda de algum aparelho especial, um milímetro de uma régua comum for dividido em 10 partes a medição será mais exata do que apenas usando o milímetro como unidade. No entanto, isso não elimina a incerteza; apenas a diminui. A medida de uma grandeza se faz adotando-se uma medida ou convenção denominada padrão, através desta, determina-se os múltiplos e submúltiplos do padrão.

Em cada lugar do mundo se media de diferentes formas; cada maneira de medir se chamava sistema de medida. Atualmente se usa quase no mundo inteiro o Sistema Internacional de Unidades (SI), um sistema padrão. No Brasil, o sistema utilizado é o SI3 , cada sistema de unidades tem uma unidade padrão para cada medida. As medidas mecânicas, suas unidades-padrão e seus símbolos, estão contidas a seguir:

UNIDADES-PADRÃO DO SI
Medidas	Unidade	Símb.
Comprimento	metro	m
Massa	quilograma	kg
Tempo	segundo	s
Força	newton	N
Potência	watt	W
Trabalho	joule	J
Energia	joule	J
Momento linear	quilograma-metros por segundo	kg.m/s
Momento de inércia	quilograma-metro ao quadrado	kg.m²
Torque	Newton-metro	N.m

Estática[editar | editar código-fonte]

Ver artigo principal: Estática

Estuda as forças atuantes em um corpo em equilíbrio estático4 .

Utiliza conceitos fundamentais como espaço, tempo, massa e força, bem como premissas (princípios ou axiomas) como o da resultante (todas as forças aplicadas sobre um objeto equivalem à sua soma), o da gravitação e as três leis de Newton. Chega-se a resultados como o equilíbrio mecânico e a formulações mais avançadas como o do momento de alavanca.

Cinemática[editar | editar código-fonte]

Ver artigo principal: Cinemática

Estuda o movimento, sem levar em consideração as forças atuantes e a massa do corpo.

Trajetória;
Espaço (módulo do comprimento da trajetória);
Velocidade;
Aceleração;
Tempo.

Dinâmica[editar | editar código-fonte]

Ver artigo principal: Dinâmica

Fundamentada na segunda lei de Newton ou princípio fundamental da dinâmica5 , estuda o movimento tendo em conta as causas deste (genericamente forças).

Princípios da conservação de energia mecânica clássica[editar | editar código-fonte]

Ver artigo principal: Lei da conservação da energia

Estuda a conservação de energia mecânica clássica nas variações de energia de corpos de um sistema isolado através fenômenos mecânicos do cotidiano.

Outros ramos[editar | editar código-fonte]

A mecânica divide-se ainda em vários ramos, conforme o estado físico dos corpos a que se aplicam forças. estática e dinâmicaestudam corpos no estado sólido. A mecânica dos fluidos estuda os outros estados físicos.

Fluidos
- Líquidos
  - Hidrostática
  - Hidrodinâmica
- Gases
  - Aerostática
  - Aerodinâmica

Extensões[editar | editar código-fonte]

Mecânica analítica (mecânica lagrangiana e mecânica hamiltoniana) — equivalente às leis de Newton e às suas consequências, são práticas para a resolução de problemas complexos que a aplicação direta da mesma, pois lida preferencialmente com grandezas escalares (como energia cinética e potencial) e não vetoriais (como força).
Mecânica relativista — transcendente à mecânica clássica, lida com objetos que se movem a velocidades relativísticas (de valor próximo da velocidade da luz) e com a dinâmica de energia.
Mecânica quântica — trata de sistemas de reduzidas dimensões (onde a troca de energia é quantizada e não contínua)
teoria do campo quântico — trata de sistemas que têm ambas as propriedades (altas velocidades e troca de energia quantizada).

A mecânica clássica é uma teoria para a dinâmica de matéria, em verdade a primeira teoria nesta área a se consolidar, e também a primeira teoria física a se mostrar, historicamente, completamente coerente. A mecânica clássica é assim compatível com as outras teorias clássicas fundamentadas na dinâmica da matéria, a citar a termodinâmica e gravitação universal. Entretanto ela não é uma teoria para a descrição da dinâmica de energia, ou de matéria e energia, sendo a mecânica clássica em vários pontos incompatível com a teoria clássica que lida com a dinâmica da energia pura, o eletromagnetismo. A relatividade restrita é uma extensão que permite a compreensão da dinâmica de matéria e energia juntas, mas exclui a gravitação de seu campo de estudo, valendo nos casos onde o campo gravitacional é essencialmente nulo. A teoria que permite a compreensão da dinâmica da matéria e energia junto com a gravitação é a teoria geral da relatividade. Todas estas teorias valem em um mundo "clássico" onde a troca de energia não équantizada e sim contínua. Se admitimos a quantização da energia, fato no mundo microscópico das partículas fundamentais, a extensão da mecânica clássica é a mecânica quântica. As demais teorias clássicas seguem o mesmo caminho, geralmente tendo suas versões quânticas (não necessariamente já completamente estruturadas).

Símbolos[editar | editar código-fonte]

Símbolo6	Significado	Símbolo	Significado
$\mathrm{A, B}\ldots$	pontos no espaço, curvas, superfícies e sólidos	$\Delta\,a$	aumento da variável $a$ durante um intervalo de tempo
$\mathrm{A, B}\ldots \mathrm{a, b}\ldots$	unidades	$\vec{e}_x, \vec{e}_y, \vec{e}_z$	versores cartesianos nos eixos x, y e z
$A, B\ldots a, b\ldots$	variáveis	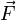$\vec{F}$	força
$\vec{A},\vec{B}\ldots \vec{a}, \vec{b}\ldots$	vetores	$\vec{F}_\mathrm{c}, \vec{F}_\mathrm{e}$	forças de atrito cinético e estático
$\vec{a}\cdot\vec{b}$	produto escalar entre vetores	$\vec{F}_\mathrm{e}$	força elástica
$\vec{a}\times\vec{b}$	produto vetorial entre vetores	$a_x, a_y, a_z$	Componentes cartesianas da aceleração
$\frac{\mathrm{d}\,a}{\mathrm{d}\,x}$	derivada da variável a em função de x	$e$	número de Euler (base dos logaritmos naturais)
$\dot{a}, \ddot{a}\ldots$	derivadas da variável a em função do tempo	$b$	Braço de uma força
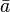$\bar{a}$	valor médio da variável a	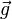$\vec{g}$	aceleração da gravidade
$a$	aceleração (módulo do vetor aceleração)	$i$	número imaginário 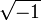$\sqrt{-1}$
$\vec{a}$	vetor aceleração	$\vec{I}$	impulso
$a_\mathrm{t}$	componentes normal e tangencial da aceleração	$\Delta\,\vec{r}$	vetor deslocamento
$C_\mathrm{D}$	coeficiente aerodinâmico do termo da pressão	$\mathcal J$	matriz jacobiana
$\vec{e}_a$	versor (vetor unitário) na direção do vetor a	$J$	joule (unidade SI de trabalho e energia)
$E_\mathrm{c}$	energia cinética	$N$	newton (unidade SI de força)
$E_\mathrm{m}$	energia mecânica	$k$	constante elástica ou coeficiente aerodinâmico do termo da viscosidade
$\vec{e}_\mathrm{n}, \vec{e}_\mathrm{t}$	versores normal e tangencial	$kg$	quilograma (unidade SI de massa)
$\mathrm{m}$	massa	$m$	metro (unidade SI de comprimento)
$\vec{M}_\mathrm{O}$	momento de uma força em relação a um ponto O	$M$	momento de um binário
$W$	trabalho	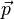$\vec{p}$	quantidade de movimento
$\vec{P}$	peso	$U$	energia potencial
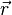$\vec{r}$	vetor posição	$U_\mathrm{e}$	energia potencial elástica
$R$	raio de curvatura de uma trajetória	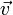$\vec{v}$	vetor velocidade
$R, \theta, z$	coordenadas cilíndricas	$\alpha$	aceleração angular
$R_\mathrm{n}$	reação normal	$\mu_\mathrm{e}, \mu_\mathrm{c}$	coeficientes de atrito estático e cinético
$s$	distância percorrida	$\pi$	valor em radianos de um ângulo de 180 $^\circ$
$\mathrm{s}$	segundo (unidade SI de tempo)	$\theta$	ângulo de rotação dos versores normal e tangencial
$T$	período num movimento circular uniforme	$\rho$	massa volúmica
$\lambda$	valor próprio de uma matriz	$\omega$	velocidade angular
$\Omega$	frequência angular	$\vec{u}$	velocidade de fase