Lei de Ohm

A diferença de potencial, V, dividido pela corrente eléctrica, I , é resistência do resistor, R, que é denominada de Lei de Ohm: V = IR
Índice
Primeira lei de Ohm
Quando essa lei é verdadeira num determinado condutor mantido à temperatura constante, este denomina-se condutor ôhmico. A resistência de um dispositivo condutor é dada pela fórmula:
ou

onde:
 é a diferença de potencial elétrico (ou tensão, ou ddp) medida em volt (V);
é a diferença de potencial elétrico (ou tensão, ou ddp) medida em volt (V); é a intensidade da corrente elétrica medida em ampère (A) e
é a intensidade da corrente elétrica medida em ampère (A) e é a resistência elétrica medida em ohm (Ω).
é a resistência elétrica medida em ohm (Ω).
Entretanto, para alguns materiais, por exemplo os semicondutores, a resistência elétrica não é constante, mesmo que a temperatura seja, ela depende da diferença de potencial
 . Estes são denominados condutores não ôhmicos. Um exemplo de componente eletrônico que não obedece à lei de Ohm é o diodo.
. Estes são denominados condutores não ôhmicos. Um exemplo de componente eletrônico que não obedece à lei de Ohm é o diodo.Interpretação da resistência elétrica
A resistência elétrica pode ser entendida como a dificuldade de se estabelecer uma corrente elétrica num determinado condutor. Por exemplo, um fio de nicromo precisa ser submetido à uma diferença de potencial de 300V para que seja estabelecida uma corrente de 1A, enquanto um fio de tungstênio precisa ser submetido à apenas 15V para que nele se estabeleça a mesma corrente. Isto significa que a resistência elétrica do nicromo é maior do que a do tungstênio:3Segunda lei de Ohm
A segunda lei de Ohm diz que a resistência elétrica de um condutor homogêneo e de seção transversal constante é proporcional ao seu comprimento , inversamente proporcional à sua área transversal
, inversamente proporcional à sua área transversal  e depende da temperatura e do material de que é feito o condutor:3
e depende da temperatura e do material de que é feito o condutor:3 chama-se resistividade elétrica e é característica do material e da temperatura. Sua unidade de medida é o ohm-metro (
chama-se resistividade elétrica e é característica do material e da temperatura. Sua unidade de medida é o ohm-metro ( m). Ela é inversamente proporcional condutividade elétrica
m). Ela é inversamente proporcional condutividade elétrica  .
.Formulação microscópica
Em um condutor metálico isolado, os elétrons estão num estado de movimento aleatório, não apresentando deslocamente preferencial, em média, em nenhuma direção. Se este condutor tem seus terminais ligados aos de uma bateria, um campo elétrico é criado em todos os pontos no interior do condutor e atua sobre os
elétrons de forma a produzir um movimento de arrasto, que é a corrente
elétrica. Em condutores ôhmicos, o vetor densidade de corrente elétrica
é criado em todos os pontos no interior do condutor e atua sobre os
elétrons de forma a produzir um movimento de arrasto, que é a corrente
elétrica. Em condutores ôhmicos, o vetor densidade de corrente elétrica 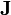 , cujo módulo é igual à corrente elétrica dividida pela área de seção transversal,
, cujo módulo é igual à corrente elétrica dividida pela área de seção transversal,  (quando a corrente é uniformemente distribuída pelo condutor), é proporcional ao campo elétrico
(quando a corrente é uniformemente distribuída pelo condutor), é proporcional ao campo elétrico  4 . O fator de proporcionalidade entre a densidade de corrente e o campo elétrico é a condutividade elétrica
4 . O fator de proporcionalidade entre a densidade de corrente e o campo elétrico é a condutividade elétrica  :
: . Pode-se dizer também que um material condutor obedece à lei de Ohm se a condutividade
. Pode-se dizer também que um material condutor obedece à lei de Ohm se a condutividade  for independente de
for independente de  e de
e de 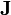 .
.A unidade de medida da condutividade é o siemens por metro (S/m). Materiais que conduzem melhor a corrente elétrica são aqueles que possuem os valores mais altos de
 . A prata, o cobre e o alumínio, por exemplo, são bons condutores, enquanto a mica e o vidro são maus condutores 1 .
. A prata, o cobre e o alumínio, por exemplo, são bons condutores, enquanto a mica e o vidro são maus condutores 1 .A relação macroscópica da lei de Ohm a partir da relação microscópica
 pode ser obtida da relação microscópica
pode ser obtida da relação microscópica  a partir do seguinte exemplo 5 .
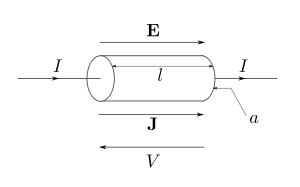
a partir do seguinte exemplo 5 .Considere um segmento de fio condutor de comprimento
 e seção reta
e seção reta  , com uma corrente
, com uma corrente  .
Para que o campo elétrico não varie apreciavelmente, o segmento do fio
deve ser muito pequeno. Sendo o campo elétrico dirigido da esquerda para
a direita, o potencial é mais baixo neste lado do que no outro, de
forma que se tem
.
Para que o campo elétrico não varie apreciavelmente, o segmento do fio
deve ser muito pequeno. Sendo o campo elétrico dirigido da esquerda para
a direita, o potencial é mais baixo neste lado do que no outro, de
forma que se tem é o módulo do campo elétrico. A corrente no condutor é igual ao produto da densidade de corrente pela área de seção reta:
é o módulo do campo elétrico. A corrente no condutor é igual ao produto da densidade de corrente pela área de seção reta: por
por  , obtém-se
, obtém-se
A expressão entre parênteses pode ser definida como
Variação da resistividade com a temperatura
Nos metais, os elétrons da última camada eletrônica estão fracamente ligados a átomos individuais, podendo mover-se livremente. Quando a temperatura aumenta, a amplitude do movimento dos íons da rede cristalina também aumenta, o que dificulta a locomoção dos elétrons livres. Em outras palavras, isto quer dizer que a resistividade aumenta com a temperatura. Para uma ampla gama de substâncias, esse aumento é linear, dentro de uma larga faixa de temperaturas. Isto pode ser descrito pela seguinte equação 6 : é a resistividade à temperatura
é a resistividade à temperatura  ,
, é a resistividade à temperatura
é a resistividade à temperatura  e
e é o coeficiente de temperatura da resistividade e é positivo para os metais.
é o coeficiente de temperatura da resistividade e é positivo para os metais.
A resistividade de alguns condutores desaparece bruscamente abaixo de uma temperatura crítica, quando estes são resfriados, podendo manter uma corrente por muito tempo sem necessidade do uso de baterias. Esse fenômeno é chamado de supercondutividade e foi divulgado pela primeira vez em 1911 pelo físico holandês Heike Kamerlingh Onnes 2 .
Modelo microscópico clássico para a condutividade elétrica de metais
Em um metal, os elétrons que não estão presos aos átomos e podem movimentar-se livremente são chamados elétrons de condução 4 . Classicamente, a velocidade quadrática média de agitação térmica dos elétrons à temperatura pode ser estimada via Teorema da equipartição 6 :
pode ser estimada via Teorema da equipartição 6 : é o valor médio do quadrado da velocidade dos elétrons devido a agitação térmica,
é o valor médio do quadrado da velocidade dos elétrons devido a agitação térmica, é a massa do elétron e
é a massa do elétron e é a constante de Boltzmann.
é a constante de Boltzmann.
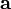 devido à força elétrica
devido à força elétrica  , onde
, onde  é a carga do elétron em módulo. De acordo com a segunda lei de Newton,
é a carga do elétron em módulo. De acordo com a segunda lei de Newton,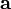 é a aceleração do elétron.
é a aceleração do elétron.
Entretanto, as frequentes colisões dos elétrons que acontecem ao longo do fio fazem com que eles sofram desaceleração. Desta forma, mesmo que eles estejam se acelerando entre as colisões, o resultado global é uma velocidade média constante. Após uma colisão, essa velocidade varia em média de
 , em que
, em que  é o tempo médio entre duas colisões, representado por
é o tempo médio entre duas colisões, representado por  e
e  é a distância média percorrida pelo elétron entre duas colisões, conhecida como livre caminho médio.
é a distância média percorrida pelo elétron entre duas colisões, conhecida como livre caminho médio.O valor médio da velocidade devida a ação do campo elétrico será dada, então, por
 pode ser expressa em termos da densidade de corrente elétrica
pode ser expressa em termos da densidade de corrente elétrica 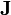 :
: é o número de elétrons livres por unidade de volume e o sinal de menos é
devido ao fato de que as cargas em movimento são negativas. Igualando
este resultado ao anterior, obtém-se
é o número de elétrons livres por unidade de volume e o sinal de menos é
devido ao fato de que as cargas em movimento são negativas. Igualando
este resultado ao anterior, obtém-se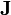 é proporcional ao campo elétrico
é proporcional ao campo elétrico  , assim como na lei de Ohm. Entretanto, não se pode afirmar que a quantidade
, assim como na lei de Ohm. Entretanto, não se pode afirmar que a quantidade  seja um bom modelo para a condutividade elétrica de metais, já que a
dedução apresentada aqui foi baseada em argumentos puramente clássicos.
Por exemplo, experiências mostram que a altas temperaturas, a
resistividade elétrica desses materiais varia linearmente com a
temperatura e o modelo aqui apresentado implica numa variação
proporcional a
seja um bom modelo para a condutividade elétrica de metais, já que a
dedução apresentada aqui foi baseada em argumentos puramente clássicos.
Por exemplo, experiências mostram que a altas temperaturas, a
resistividade elétrica desses materiais varia linearmente com a
temperatura e o modelo aqui apresentado implica numa variação
proporcional a 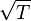 devido ao termo
devido ao termo  no denominador da expressão anterior. Ainda assim, o modelo clássico de
movimento de arrasto na presença de campo elétrico superposto ao
movimento aleatório térmico devido a colisões com átomos do material,
conhecido como modelo de Drude,
apresenta os ingredientes básicos que definem a condutividade. Um
tratamento adequado para o problema da condutividade elétrica em metais é
dado pela Mecânica Quântica.
no denominador da expressão anterior. Ainda assim, o modelo clássico de
movimento de arrasto na presença de campo elétrico superposto ao
movimento aleatório térmico devido a colisões com átomos do material,
conhecido como modelo de Drude,
apresenta os ingredientes básicos que definem a condutividade. Um
tratamento adequado para o problema da condutividade elétrica em metais é
dado pela Mecânica Quântica.Potência dissipada num resistor
Quando um resistor é percorrido por uma corrente elétrica , devida a uma tensão
, devida a uma tensão  fornecida por uma fonte de energia, ele se aquece. Esse aquecimento, chamado de efeito Joule,
é resultado da transformação da energia que vem da fonte em energia
térmica no resistor. A energia transformada em calor por unidade de
tempo é a potência dissipada2 e é calculada pela equação
fornecida por uma fonte de energia, ele se aquece. Esse aquecimento, chamado de efeito Joule,
é resultado da transformação da energia que vem da fonte em energia
térmica no resistor. A energia transformada em calor por unidade de
tempo é a potência dissipada2 e é calculada pela equaçãoUsando
 , obtém-se
, obtém-se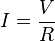 :
:







![\rho = \rho_{0}[{1} + {\alpha \,(T - T_{0})}]](http://upload.wikimedia.org/math/7/7/1/77197eda287c59863afa9456e745e531.png)












Nenhum comentário:
Postar um comentário