Equação
Em matemática, uma equação é uma afirmação que estabelece uma igualdade entre duas expressões matemáticas.1 2
São exemplos de equações as seguintes igualdades:
 e
e  são as incógnitas de suas equações. A incógnita de uma equação é o número desconhecido que se quer descobrir.
são as incógnitas de suas equações. A incógnita de uma equação é o número desconhecido que se quer descobrir.A equação
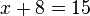 pode ser interpretada como uma pergunta: "qual o número que somado com 8 dá 15?". Não é necessário nenhum método ou fórmula para encontrar o valor de
pode ser interpretada como uma pergunta: "qual o número que somado com 8 dá 15?". Não é necessário nenhum método ou fórmula para encontrar o valor de  nesse caso: basta pensar um pouco para se chegar ao resultado
nesse caso: basta pensar um pouco para se chegar ao resultado  .
.Resolver uma equação é encontrar todos os valores possíveis para a incógnita que tornem a igualdade verdadeira.3 As equações mostradas nos exemplos acima podem ser interpretadas e resolvidas facilmente: o número que subtraído de 10 é igual a 4 é
 ; o número que, ao ser multiplicado por 3, resulta em 18 é
; o número que, ao ser multiplicado por 3, resulta em 18 é  .
.Uma solução da equação também é chamada raiz da equação.
Algumas equações matemáticas descrevem, na verdade, identidades matemáticas, isto é, afirmações que são verdadeiras para todos os valores de
 ,2 como nos exemplos:
,2 como nos exemplos: , a saber,
, a saber,  e
e 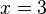 .
.Em geral, os matemáticos reservam a palavra equação exclusivamente para igualdades que não são identidades. A distinção entre esses dois conceitos pode ser bastante sutil. Por exemplo:
 e
e 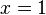 .
.Em geral, é possível perceber se se trata de uma identidade ou de uma equação pelo contexto em que a igualdade se encontra. Em alguns casos, na identidade, o sinal de igualdade (=) é trocado pelo sinal
 .
.Ideia básica para se resolver equações
Há muitas formas de se resolver equações4 mas a principal ideia, quando as incógnitas são procuradas nos conjuntos dos números inteiros, racionais, reais ou mesmo complexos é o fato que o produto de números só é igual a zero se um dos fatores for igual a zero.Assim, para se resolver a equação
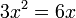 , o método mais simples e eficiente é escrever:
, o método mais simples e eficiente é escrever: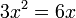 é equivalente a
é equivalente a  , que, por sua vez, pode ser escrito na forma
, que, por sua vez, pode ser escrito na forma . Como o produto só pode ser 0 se um dos fatores for igual a 0, concluímos que ou
. Como o produto só pode ser 0 se um dos fatores for igual a 0, concluímos que ou ou
ou  .
.
 ou
ou  .
.O mesmo método pode ser aplicado a equações mais difíceis, com a mesma eficiência. Portanto, para se saber resolver equações é importante, antes de mais nada, saber fatorar expressões algébricas.
Equações equivalentes
Diz-se que duas equações são equivalentes se elas têm as mesmas raízes (soluções).3 Por exemplo, considere as equações:
 e
e  . As equações (ii) e (iii) admitem apenas a solução real
. As equações (ii) e (iii) admitem apenas a solução real  . Assim sendo, as equações (i) e (ii) não são equivalentes, enquanto que as equações (ii) e (iii) são equivalentes. Escrevemos
. Assim sendo, as equações (i) e (ii) não são equivalentes, enquanto que as equações (ii) e (iii) são equivalentes. Escrevemos .
.
Como transformar uma equação em outra equivalente
Dada uma equação, as seguintes operações podem ser efetuadas sem que se modifique o conjunto-solução:
- somar um mesmo número real em cada lado da igualdade.3
- multiplicar cada lado da igualdade por uma mesma constante não nula.5
 ) e chegar à solução procurada:
) e chegar à solução procurada: ou
ou  , ou seja,
, ou seja,  ou
ou 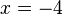 .
.Poderíamos também aplicar a função raiz quadrada a ambos os lados da equação
 :
: ou
ou  .
.Uma situação que exige mais cuidado é quando, para resolvermos uma equação algébrica, elevamos cada lado da equação ao quadrado. Ao fazermos isso, perdemos a informação sobre o sinal (positivo ou negativo) de cada membro da equação e, por isso, iremos obter outra equação, que não é equivalente à original: ela terá mais soluções. Logo, quando usamos essa técnica temos que, no final, voltar à equação original e verificar quais soluções da equação modificada são também soluções da equação original. Vejamos um exemplo: é dada a equação
 e
e 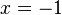 . Entretanto, testando-se na equação original tem-se, para
. Entretanto, testando-se na equação original tem-se, para  :
: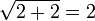 , que é verdadeira. Já para
, que é verdadeira. Já para 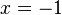 , a igualdade é falsa, já que
, a igualdade é falsa, já que . Logo, a equação
. Logo, a equação  admite apenas uma solução, a saber,
admite apenas uma solução, a saber,  .
.-
Equações com mais de uma incógnita
Uma equação pode ter mais de uma incógnita, como por exemplo, a equação

 . Se permitirmos números inteiros, encontraremos infinitas soluções. Além das soluções encontradas anteriormente, os pares
. Se permitirmos números inteiros, encontraremos infinitas soluções. Além das soluções encontradas anteriormente, os pares  são alguns exemplos neste caso. Se admitirmos soluções formadas por
números reais, o conjunto das soluções da equação aumenta
consideravelmente: o conjunto de todos os pares ordenados que satisfazem à equação pode ser representado no plano cartesiano por uma reta, mais precisamente, a reta determinada pelos pontos de coordenadas (0,7) e (7, 0).
são alguns exemplos neste caso. Se admitirmos soluções formadas por
números reais, o conjunto das soluções da equação aumenta
consideravelmente: o conjunto de todos os pares ordenados que satisfazem à equação pode ser representado no plano cartesiano por uma reta, mais precisamente, a reta determinada pelos pontos de coordenadas (0,7) e (7, 0).O exemplo acima deve ajudar a compreender a importância de, ao se formular uma equação, definirmos qual o conjunto universo, ou seja, qual o conjunto em que vamos procurar as soluções. Quando o conjunto universo não é dado, subentende-se que se deva procurar soluções no conjunto dos números reais.
Uma equação que seja equivalente a outra escrita na forma
 em que
em que  são constantes é uma equação de reta, justamente porque o conjunto de todas as suas soluções reais é representado por uma reta no plano cartesiano.
são constantes é uma equação de reta, justamente porque o conjunto de todas as suas soluções reais é representado por uma reta no plano cartesiano.Uma equação com três incógnitas tem o conjunto solução representado no espaço tridimensional. Por exemplo, as soluções da equação
 são triplas de números que podem ser vistos como coordenadas de pontos do espaço. Fixado um sistema cartesiano tridimensional, as soluções dessa equação determinam o plano que passa pelos pontos de coordenadas
são triplas de números que podem ser vistos como coordenadas de pontos do espaço. Fixado um sistema cartesiano tridimensional, as soluções dessa equação determinam o plano que passa pelos pontos de coordenadas  .
.Equações com mais de uma variável começaram a ser estudadas sistematicamente a partir das ideias de Descartes e deram início ao que hoje chamamos de Geometria analítica. A Geometria analítica tanto ajuda a resolver problemas algébricos por meio da Geometria, como a resolver problemas geométricos por meio da Álgebra.
Tipos de equações
As equações com uma incógnita mais simples são as chamadas equações lineares. São as equações equivalentes a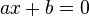 em que as letras
em que as letras  e
e  representam números fixados (as constantes). O número
representam números fixados (as constantes). O número  é chamado coeficiente de
é chamado coeficiente de  . Equações lineares têm exatamente uma solução real.
. Equações lineares têm exatamente uma solução real.Equações quadráticas são as equações que podem ser colocadas na forma
 por operações elementares. Essas equações podem ter até duas soluções reais distintas.
por operações elementares. Essas equações podem ter até duas soluções reais distintas.Equações do terceiro grau, também chamadas equações cúbicas são as equações que podem ser colocadas na forma
 . Tais equações possuem até três soluções reais distintas.
. Tais equações possuem até três soluções reais distintas.Mais geralmente, equações polinomiais de grau n são as equações da forma
Equações algébricas são as que são escritas apenas usando-se adição, multiplicação divisão, raízes ou potências de expressões polinomiais.6 São exemplos de equações algébricas as seguintes:
Outra divisão das equações algébricas é entre elas serem numéricas ou literais. No caso das equações algébricas numéricas, todas quantidades conhecidas são representadas por números, no caso das literais, algumas podem ser representadas por letras (constantes).José Adelino Serrasqueiro, Tratado de Álgebra Elementar, p. 82, [ver wikisource]</ref>
As equações que não são algébricas são chamadas de transcendentes.6 Há muitos outros tipos de equações. Um tipo bastante estudado no ensino médio são as funções trigonométricas, que são equações em que pelo menos em um dos lados da igualdade aparece uma função trigonométrica. Por exemplo,
 é uma equação trigonométrica que tem infinitas soluções reais.
é uma equação trigonométrica que tem infinitas soluções reais.Em geral, se
 é uma função real podemos considerar a equação
é uma função real podemos considerar a equação  . Suas soluções são os zeros de
. Suas soluções são os zeros de  . Geometricamente, os zeros de uma função são as abscissas dos pontos em que o gráfico de
. Geometricamente, os zeros de uma função são as abscissas dos pontos em que o gráfico de  cruza o eixo dos x.
cruza o eixo dos x.Equações mais gerais
Até aqui vimos exemplos de equações em que a(s) incógnita(s) era(m) número(s) (inteiro, racional, real, complexo). Mas há equações em que a incógnita pode ser outro objeto matematico, por exemplo, uma função. Por exemplo:- Determinar as possíveis funções contínuas
 tais que:
tais que:
- Determinar as possíveis funções contínuas
 tais que:
tais que:
- Equações diferenciais possuem uma função como uma incógnita e pelo menos uma das expressões da equação envolve a derivada de ordem 1 ou maior desta função:
- Analogamente, equações integrais possuem como incógnita uma função e pelo menos um dos lados da igualdade envolve integrais:
- Sistemas de equações são duas ou mais expressões que devem ser resolvidas simultaneamente:
 com a hipérbole
com a hipérbole  , a saber, os pontos P e Q de coordenadas
, a saber, os pontos P e Q de coordenadas  e
e  , respectivamente.
, respectivamente.






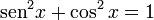

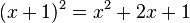

















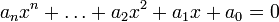
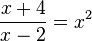




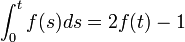
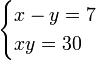
Nenhum comentário:
Postar um comentário