Teoria
eoria, do grego θεωρία , é o conhecimento descritivo puramente racional. O substantivo theoría significa ação de contemplar, olhar, examinar, especular1 . Também pode ser entendido como forma de pensar e entender algum fenômeno a partir da observação. Na Grécia antiga, teoria significava "festa solene, procissão ou embaixada que as cidades helênicas enviavam para representá-las nos jogos olímpicos ou para consultar os oráculos".
O termo é aplicado a diversas áreas do conhecimento, sendo que em cada área possui uma
definição específica.
Em ciência, a definição de teoria científica difere bastante da acepção de teoria em
senso comum, o de simples especulação; o conceito moderno de teoria científica estabelece-se, entre outros, como uma resposta ao
problema da demarcação entre o que é efetivamente científico e o que não o é.
Teoria científica
Uma definição científica de teoria é a de que ela é uma
síntese aceita de um vasto campo de conhecimento, consistindo-se de
hipóteses
necessariamente falseáveis - mas não por isto erradas, dúbias ou tão
pouco duvidosas - que foram e são permanentemente e devidamente
confrontadas entre si e com os fatos científicos, fatos estes que
integram um conjunto de evidências que, juntamente com as hipóteses,
alicerçam o conceito de teoria científica. As hipóteses, em casos
específicos, devido à simplicidade e ampla abrangência, podem ser
elevadas ao status de
leis.
Ressalta-se aqui portanto que
uma "teoria científica" é o conjunto indissociável dos dois subconjuntos: o subconjunto de fatos naturais, evidências necessariamente verificáveis mas, ao contrário do que muitos pensam, não obrigatoriamente reprodutíveis,
e um subconjunto de hipóteses científicas adequadas à descrição destes fatos,
de ideias necessariamente falseáveis, testáveis (e testadas) frente às
evidências e que, junto àquele, dão corpo ao conceito de teoria
científica.
É comum associar-se o conceito de teoria apenas a uma ou a um
conjunto de ideias que tenta prever com alto grau de exatidão os
fenômenos da natureza. Em verdade, vários cientistas acabam muitas vezes
por aderir a esta conotação. Contudo em ciência o conjunto de fatos
faz-se sempre presente e indispensável, e este está, mesmo quando não
explicitamente considerado, certamente subentendido. Sempre que
observamos algum fato novo que venha a contrariar a teoria vigente,
deve-se abandonar as ideias conflitantes e jamais ignorar o fato:
modifica-se a teoria, de forma a integrá-los à mesma, fato e novas
ideias. Conclui-se que as teorias evoluem em virtude da descoberta de
novos fatos, que necessariamente passam a integrar a versão evoluída da
mesma.
Há também de se sublinhar que a ciência, ao buscar uma simplificação
da sistematização do conhecimento produzido, divide-se em áreas e mesmo
em disciplinas por mera formalidade. A ciência entretanto é única. Há um
único conjunto de fatos naturais, sobre o qual as mais variadas teorias
científicas válidas se assentam. Apesar de um subconjunto de fatos em
particulares ser destacado para integrar determinada teoria, nenhum
paradigma válido - nenhuma teoria em vigor - pode conter ideias que
contrastem com qualquer dos demais fatos científicos conhecidos,
independente da área científica da qual este seja proveniente ou da área
na qual este seja (mais) relevante. Se isto ocorrer, a teoria DEVE ser
reformulada; esta encontra-se impelida a evoluir. Em outras palavras,
citando um exemplo de validade significativa frente ao contexto
cultural, as ideias da teoria da
termodinâmica e da teoria da
evolução, ao contrário do que alguns leigos científicos afirmam, sendo ambas paradigmas válidos hoje,
não
podem se contradizer e não se contradizem; tão pouco podem contradizer
ou contradizem os fatos hoje conhecidos, sejam eles oriundos da física,
da química, ou da biologia, ou de qualquer outra cadeira científica.
Para
Karl Popper,
deve-se submeter criticamente as teorias à prova dos fatos e
selecioná-las de acordo com os resultados obtidos, através da dedução
lógica e da comparação dos resultados. Popper indica quatro diferentes linhas para submeter uma teoria à prova:
- Comparação lógica das conclusões umas com as outras, para se testar a coerência interna do sistema;
- Investigação da forma lógica da teoria, com objetivo de determinar
se ela apresenta caráter de uma teoria empírica, científica ou
tautológica;
- Comparação com outras teorias, para ver se há avanço de ordem científica ;
- Comparação da teoria por meio de aplicações empíricas das conclusões que dela se possam deduzir.2
No
pensamento científico o fato sempre é superior à
ideia, sendo que o fato sempre pode
destruir
- corretamente dizendo, tornar falsa - a ideia científica. Por isso,
por ser uma teoria científica sempre formada a partir de hipóteses
testáveis e falseáveis, há sempre a possibilidade de aparecer um fato
que venha a destruir a visão nela encerrada e até então válida e atual.
Decorre que teorias científicas jamais são provadas pois é impossível
garantir-se que nunca se descobrirá um novo fato que venha a contradizer
alguma de suas ideias até então válidas. Entretanto, algumas teorias
estão tão bem corroboradas por uma quantidade tão grande de fatos que,
na prática, é pouco provável conceber que estas sejam falseadas.
Entretanto esta possibilidade é inerente e indissociável de qualquer
teoria que se diz científica, não devido aos fatos, mas às ideias
associadas à mesma.
Explicitamente, segue-se que, em acordo com a definição moderna de teoria científica - notoriamente atrelada ao
positivismo de Popper e outros -
não existe teoria científica, nem uma sequer, provada 3 .
Isto certamente é difícil de se assimilar em sua abrangência. A
exemplo, mesmo após as considerações presentes, se alguém lhe
perguntasse: "A teoria da gravidade foi provada?", o que você
responderia? Certamente hesitaria em dizer que não! Contudo, deve-se
lembrar que a teoria da gravidade
não constitui-se apenas pela evidência
empírica - observacional - de que
massa
atrai massa. Isto, verifica-se! E esta evidência faz certamente parte
da teoria gravitacional, contudo não há teorias sem ideias que descrevam
e expliquem os fatos. Vê-se que a teoria da gravidade
não encontra-se provada ao considerar-se a
evolução histórica da mesma: da
teoria proposta por Newton até a atual, a
Relatividade Geral - proposta por
Einstein - há certamente uma grande discrepância na área ideológica.
O pensamento científico está sempre evoluindo e sempre preserva a
melhor teoria, geralmente a mais simples e abrangente, através da
chamada "
Navalha de Ockham".
Estabelecido o conceito de teoria científica, várias são, entretanto,
as opiniões sobre a abrangência e precisão da mesma para descrever o
universo como um todo, principalmente na área da
filosofia ou mesmo dentro da
filosofia da ciência.
Janice Moulton
defende que as teorias científicas incorporam valores, porque advogam
uma forma de descrever o mundo em detrimento de outras, e que mesmo as
observações de fato são feitas a partir de algum ponto de vista ou
teoria sobre o mundo, já pressuposta.
4
Thomas Kuhn defende que mesmo a argumentação usada na ciência não é livre de valorações, ou certa. A ciência envolve um sistema, ou
paradigma,
não apenas de generalizações e conceitos, mas de crenças sobre a
metodologia e critérios de avaliação da investigação: sobre o que são
boas questões, o que sejam desenvolvimentos adequados de uma teoria, ou
métodos de investigação aceitáveis. Uma teoria substitui outra, não
porque funcione, com sucesso, como premissa maior num maior número de
deduções, mas porque responde a algumas questões que a outra teoria não
responde. As mudanças de teoria ocorrem porque uma teoria satisfaz mais
do que outra, porque as questões a que dá resposta são consideradas mais
importantes. A investigação feita sob um paradigma não é feita para
falsificar uma teoria, mas para preencher e desenvolver conhecimento
para o qual o paradigma fornece um quadro de trabalho. O procedimento
envolvido no desenvolvimento e substituição de um paradigma não é
simplesmente dedutivo, e não existe, provavelmente, uma caracterização
única adequada de como tal procedimento funciona. Isto não significa que
ele seja irracional, ou não mereça ser estudado, mas apenas que não
existe uma caracterização universal simples do que seja uma boa
argumentação científica.
5
Contudo, implicações filosóficas à parte
6 7 , uma teoria científica obedece necessariamente a um método em sua elaboração, o
método científico.
Este método de trabalho é cíclico, exigindo confronto permanente entre
as ideias e os fatos que integram a teoria, o que, ao final, resulta na
veracidade das afirmações abaixo:
-
Opiniões pessoais, quem quer que as emita, NÃO constituem fatos em uma teoria científica8
. As opiniões, se testáveis e falseáveis mediante os fatos, constituem,
quando muito, hipóteses científicas, ideias dentro da teoria . Neste
contexto o papel da autoridade em ciência, mesmo que ainda certamente
relevante ao contexto científico, certamente difere em muito daquele
exercidos pelas demais autoridades de outras áreas sociais, como a
filosofia: em um debate científico acirrado, os FATOS, e não a
autoridade, decidem quais ideias científicas são válidas ou quais são
inválidas.
-
Crença não constitui fato em uma teoria 9
. Fato é algo necessariamente verificável, embora não necessariamente
reprodutível. Crença também não constitui uma hipótese científica pois,
pela própria definição de crença, trata-se de uma proposição que não
fundamenta-se em fatos verificáveis; não há fatos que as corroborem.
-
Uma teoria, apesar de necessariamente falseável em virtude das
ideias que a compõem, não é algo duvidoso, descartável ou tão pouco
incorreto10
. Ela é a melhor, mais honesta, e talvez a única maneira racionalmente
aceitável de se descrever o que se conhece do mundo natural até a data
de sua validade
11 .
-
Uma teoria científica não é uma crença 12 13
. Não se acredita em uma teoria. Se corrobora uma teoria com fatos, ou,
em caso contrário, se demonstra que a mesma é falsa mediante a
falsificação de suas ideias, feita necessariamente por contradição com
um novo fato até então desconhecido, e não por contradição com outra
ideia, (ressalvado-se aqui a natureza científica das ideias em questão e
a harmonia lógica inerente, certamente).
Equívocos sobre teorias científicas
Muitas vezes as pessoas se confundem sobre a definição de uma teoria. Nossos
dicionários trazem o significado que corresponde a uma visão popular de uma teoria, o que seria equivalente a uma
hipótese, ou definindo de uma forma ainda melhor, uma
especulação, algo duvidoso, incerto. No entanto, na
Ciência,
uma hipótese não é o mesmo que teoria, apesar de integrá-la quando
satisfaz a condição de ser testável e falseável frente aos fatos, e tão
pouco teoria é algo duvidoso, apesar de necessariamente falsificável.
Há também uma confusão relativa à análise do que poderia se chamar de
"grau de confiabilidade" que uma teoria apresenta. Muitas pessoas
acreditam que uma
lei científica possuiria um grau maior de comprovação que uma "teoria" (aqui em acepção em "
senso comum"), mas não é isso o que ocorre. Teorias e
leis, segundo a
ciência, são definidas por
conceitos bem distintos, de naturezas diferentes. Elas não se distinguem apenas por algum tipo grau de
hierarquia.
As leis nada mais são que hipóteses científicas com ampla área de
validade e exaustivamente confrontadas frente a um número enorme de
fatos, mas ainda e nada mais que hipóteses, com um "título honorífico",
apenas. Uma teoria é definida por um conceito muito mais abrangente, que
necessita do conceito de hipótese científica e em consequência do
conceito de lei para estabelecer-se, mas não se define frente os mesmos
apenas.
Outra confusão frequente é o equívoco entre
fato e
teoria.
Teoria é composta por ideias que explicam o fato, mais especificamente o
conjunto de fatos, e portanto uma teoria deve ser construída a partir
de um conjunto de
fatos; Uma teoria é a união do conjunto de ideias e do conjunto de fatos a que estas se relacionam.
Qual seria então o papel do fato face à teoria? Ele geralmente mas
não necessariamente inicia e posteriormente constitui o alicerce da
teoria. O fato reformula e rejeita a ideia em uma teoria, na medida em
que qualquer teoria é passível de modificação; ele redefine e justifica a
teoria, levando a uma melhora constante dos conceitos por ela
propostos.
Não se pode jamais afirmar, como muitos fazem-no, que uma teoria é um
fato,
ou que se transforma, quando provada, em fato. Pode ocorrer que leis
científicas possuam o mesmo "nome" que as teorias associadas. E há fatos
que são também confundidos pelo mesmo nome da teoria a qual pertence.
Deve-se ter entretanto cuidado com estas confusões de conceitos.
Uma teoria jamais é uma expressão perfeita da realidade, mas um
modelo, em definição estrita da palavra, pelo qual a realidade conhecida
pode ser descrita, compreendida, e pelo qual a realidade ainda
desconhecida pode ser estimulada a ser descoberta.
Teoria nas ciências sociais
Segundo
Robert K. Merton,
nas ciências sociais, a palavra teoria tem sido empregada de forma
bastante diversa, incluindo quase tudo, desde as menores hipóteses de
trabalho, as amplas mas vagas e desordenadas especulações, até os
sistemas axiomáticos de pensamento, daí o cuidado que se deve ter no uso
da palavra, posto que frequentemente, obscurece a compreensão ao invés
de suscitá-la.
14
Teoria do conhecimento
"Chama-se teoria do conhecimento a um conjunto de especulações que
têm por fim determinar o valor e os limites dos nossos conhecimentos"
(A. REY - Psychologie et Philosophie). Trata-se de explicar e
interpretar os problemas que decorrem de uma análise fenomenológica do
conhecimento. Agrupados em cinco problemas particulares: as questões da
possibilidade do conhecimento, da origem do conhecimento, da essência do
conhecimento, das espécies do conhecimento e do critério de verdade.
Hipótese
Do Latim
hypothese e do Grego
hypóthesis originalmente
significa suposição. A palavra hipótese assume diferentes conotações em
virtude do contexto. Figura geralmente em dicionários - os quais
geralmente pecam em definir as acepções científicas - com o seguinte
sentido: conjunto de condições que se supõe serem verdadeiras e que são
tomadas como ponto de partida para deduções; em ciências experimentais, é
a explicação plausível dos fatos, provisoriamente adaptada, com o
principal objetivo de submetê-la à verificação metódica através da
experiência; teoria provável mas não demonstrada.
15
Para existir uma pesquisa, estudo ou investigação é preciso existir
um problema ou uma questão suscitada por um ou um conjunto de fatos
(oriundos ou não de teorias pré-existentes). Com isso elaboramos uma
hipótese. Hipótese é a tentativa que fazemos de apresentar uma solução
para um problema. Neste contexto, hipótese é muitas vezes associada a
uma solução provisória, isto é, que ainda não foi testada. Nesse sentido
é que
podemos dizer que as hipóteses são explicações provisórias que tem por objetivo fazerem-se compreender os fatos.
É o "embrião" das ideias que irão figurar posteriormente no paradigma
teórico quando aceito como válido. Nestes termos, hipótese seria o mesmo
que
conjetura.
Contudo, mesmo quando testada e exaustivamente corroborada, uma hipótese nunca deixa de ser uma hipótese. Mesmo as
leis científicas
nada mais são do que hipóteses, contudo hipóteses simples de grande
abrangência, já exaustivamente corroboradas - mas nunca provadas - por
uma quantidade enorme de evidências, que por tal merecem um título de
destaque. Nestes termos, poderíamos classificar as hipóteses, em função
de sua abrangência e da corroboração dada às mesmas, basicamente em três
grupos: o das conjeturas - hipóteses iniciais, geralmente ainda não
testadas -; o dos
axiomas ou
postulados,
hipóteses já testadas e corroboradas; e por fim, o que encerra aquelas
detentoras de título honorífico de destaque, o de lei. Contudo, nos três
grupos, todas são sempre hipóteses. O leitor deve, assim, ficar atento
ao contexto a fim de inferir a qual dos grupos pertence a hipótese em
debate.
Marco teórico
É uma afirmação teórica específica de determinado
autor. O
marco teórico
é, portanto, uma afirmação de um pesquisador de determinado campo do
conhecimento que realizou investigações e reflexões sobre determinado
tema e chegou a explicações e conclusões metódicas sobre o assunto, ou
seja,
é o ponto de vista de alguém sobre determinado assunto em particular.
Tese
Do grego
thésis, (ato de pôr), pelo latim
these, (proposição).
Tese é literalmente uma proposição que se apresenta para ser defendida como a conclusão de um teorema. Ou seja,
é a conclusão que se obtém por dedução lógica a partir de outras conclusões já testadas e admitidas como verdadeiras.
Existem basicamente três níveis para se definir a validade de uma afirmação dentro do
conhecimento científico. O mais básico é a
conjetura,
geralmente o fruto das primeiras observações e dos primeiros
raciocínios indutivos. Quando essa conjetura passa pelos testes iniciais
mostrando-se agora suportada por
fatos, ainda sem ser contudo confirmada por pesquisas independentes, esta passa a ser considerada uma
tese. A obtenção do título de
Doutor
depende geralmente da defesa de uma tese a uma banca examinadora. Por
último surge a teoria, que expressa um consenso senão de todos pelo
menos entre a maioria dos membros da comunidade científica.
Para se estabelecer uma teoria as suas afirmações devem ser não apenas corroboradas por expressivas
evidências mas sobretudo contraditas por nenhuma, e também mostrarem-se harmônicas frente ao
raciocínio lógico - raciocínio desenvolvido principalmente por processos de
dedução, não excluindo-se aqui a
indução
- tudo isto sob escrutínio de vários pesquisadores independentes. Junto
com as evidências que sustentam as afirmações, tais afirmações passam
então a integrar a teoria.
É evidente que, para a validação de qualquer teoria, é necessária a
existência de um ou mais experimentos reprodutíveis associados que
possam ser realizados por pesquisadores independentes
16 , sendo importante ressaltar que tais experimentos devem estar estruturados sob a
ótica científica.
A ausência desta possibilidade, assim como a ausência de evidências
verificáveis ou confrontos com estas impedem que qualquer tese ou mesmo
hipótese, conforme proposta, possa elevar-se ao nível de teoria.
Teoria nas comunidades acadêmicas
As comunidades acadêmicas internacionais tem como padrão registrar as
ideias e referências explícita as fatos de uma teoria científica, bem
como debates e discussões no âmbito de quais as ideias que são ou não
válidas em uma teoria em artigos completos, devidamente revisados por
pares e publicados em periódicos científicos qualificados. Há padrões
internacionais para "qualificação" destas publicações periódicas
17 18 , e há também padrões brasileiros estabelecidos com o mesmo propósito
19 20 . Especialmente, o
Qualis
está sendo utilizado para avaliação de desempenho pessoal dos
pesquisadores brasileiros. Entretanto, a publicação científica não
garante a veracidade absoluta do conteúdo publicado, como espera-se ao
falar-se de teoria, porém consagra o reconhecimento oficial de sua
existência perante as comunidades científicas como uma proposta provável
no referido momento. Por outro lado, propostas divulgadas mediante
apresentação em congresso ou simpósio, artigo em uma revista de
divulgação não científica ou revista popular, em artigo de jornal,
programa de rádio ou televisão, relatório técnico, tese, dissertação ou
monografia não publicada, etc., não são tratados como teoria científica.
Antigamente, no Brasil, havia o costume de todos os documentos
decorrentes das formas de divulgação citadas serem tratados como válidos
no que concerne às teorias científicas. Entretanto, entrando o século
XXI, o padrão internacional tem sido introduzido pouco a pouco.
Teoria segundo Hawking
De acordo com o físico teórico
Stephen Hawking, em
Uma Breve História do Tempo,
"uma boa teoria deve satisfazer a dois requisitos: Precisa descrever
com precisão um número razoável de observações, com base em um modelo
que contenha poucos elementos arbitrários; e deve prever com boa margem
de definição resultados de observações futuras". Mais especificamente em
sua área de atuação: "qualquer teoria na
física
é sempre provisória, no sentido de que é apenas uma hipótese, você
nunca pode prova-la em definitivo. Não importa quantas vezes os
resultados das experiências estejam de acordo com algumas teorias, não
se pode ter a certeza de que na próxima vez o resultado não irá
contradizê-las. Por outro lado, você pode refutar uma teoria por
encontrar uma única observação que não concorde com as suas previsões".
Teorias famosas
 |
| Teoria do Big Bang |
|
Big Bang: O Universo a partir de um ponto



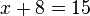




 e
e  são as
são as  .
. ; o número que, ao ser multiplicado por 3, resulta em 18 é
; o número que, ao ser multiplicado por 3, resulta em 18 é  .
.
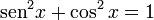

 e
e 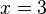 .
.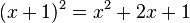

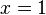 .
. .
.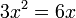 , o método mais simples e
, o método mais simples e  , que, por sua vez, pode ser escrito na forma
, que, por sua vez, pode ser escrito na forma . Como o
. Como o  ou
ou  .
. .
.

 .
.



 ) e chegar à solução procurada:
) e chegar à solução procurada:





 ou
ou  , ou seja,
, ou seja, 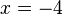 .
.



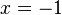 . Entretanto, testando-se na equação original tem-se, para
. Entretanto, testando-se na equação original tem-se, para 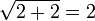 , que é verdadeira. Já para
, que é verdadeira. Já para  . Logo, a equação
. Logo, a equação 
 . Se permitirmos números inteiros, encontraremos infinitas soluções. Além das soluções encontradas anteriormente, os pares
. Se permitirmos números inteiros, encontraremos infinitas soluções. Além das soluções encontradas anteriormente, os pares  são alguns exemplos neste caso. Se admitirmos soluções formadas por
números reais, o conjunto das soluções da equação aumenta
consideravelmente: o conjunto de todos os
são alguns exemplos neste caso. Se admitirmos soluções formadas por
números reais, o conjunto das soluções da equação aumenta
consideravelmente: o conjunto de todos os  em que
em que  são constantes é uma
são constantes é uma  são triplas de números que podem ser vistos como coordenadas de pontos do espaço. Fixado um
são triplas de números que podem ser vistos como coordenadas de pontos do espaço. Fixado um  .
.
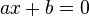 em que as letras
em que as letras  e
e  representam números fixados (as constantes). O número
representam números fixados (as constantes). O número  por operações elementares. Essas equações podem ter até duas soluções reais distintas.
por operações elementares. Essas equações podem ter até duas soluções reais distintas. . Tais equações possuem até três soluções reais distintas.
. Tais equações possuem até três soluções reais distintas.
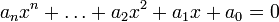
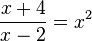

 é uma equação trigonométrica que tem
é uma equação trigonométrica que tem  é uma
é uma  . Suas soluções são os
. Suas soluções são os  . Geometricamente, os zeros de uma função são as
. Geometricamente, os zeros de uma função são as  tais que:
tais que:


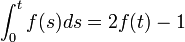
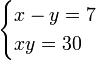
 com a
com a  , a saber, os pontos P e Q de
, a saber, os pontos P e Q de  e
e  , respectivamente.
, respectivamente.